Rangkaian Arus Searah

Rangkaian Arus Searah

Rangkaian arus searah atau direct current (DC) adalah aliran elektron dari suatu titik yang energi potensialnya tinggi ke titik lain yang energi potensialnya lebih rendah. Pada dasarnya dalam kawat penghantar terdapat aliran elektron dalam jumlah yang sangat besar, jika jumlah elektron yang bergerak ke kanan dan ke kiri sama besar maka seolah-olah tidak terjadi apa- apa. Namun jika ujung sebelah kanan kawat menarik elektron sedangkan ujung sebelah kiri melepaskannya maka akan terjadi aliran elektron ke kanan (tapi ingat, dalam hal ini disepakati bahwa arah arus ke kiri). Aliran elektron inilah yang selanjutnya disebut arus listrik. Sumber arus listrik searah biasanya adalah baterai (termasuk aki dan Elemen Volta) dan panel surya.

Arus searah dulu dianggap sebagai arus positif yang mengalir dari ujung positif sumber arus listrik ke ujung negatifnya. Pengamatan-pengamatan yang lebih baru menemukan bahwa sebenarnya arus searah merupakan arus negatif (elektron) yang mengalir dari kutub negatif ke kutub positif. Aliran elektron ini menyebabkan terjadinya lubang-lubang bermuatan positif, yang "tampak" mengalir dari kutub positif ke kutub negatif.

1. Arus Listrik

Pada dasarnya rangkaian listrik dibedakan menjadi dua, yaitu rangkaian listrik terbuka dan rangkaian listrik tertutup. Rangkaian listrik terbuka adalah suatu rangkaian yang belum dihubungkan dengan sumber tegangan, sedangkan rangkaian listrik tertutup adalah suatu rangkaian yang sudah dihubungkan dengan sumber tegangan.

Pada rangkaian listrik tertutup, terjadi aliran muatan-muatan listrik. Aliran muatan listrik positif identik dengan aliran air. Arus listrik mengalir dari potensial tinggi ke potensial rendah atau dari kutub (+) ke kutub (-). Sedangkan muatan electron mengalir dari potensial rendah ke potensial tinggi.

Perhatikan gambar di bawah ini !

Dua buah benda bermuatan masing-masing A dan B dihubungkan dengan sebuah penghantar. Bila potensial A lebih tinggi dari pada potensial B, maka arus akan mengalir dari A ke B. Arus ini mengalir dalam waktu yang sangat singkat. Setelah potensial A sama dengan potensial B maka arus berhenti mengalir.

2. Kuat Arus Listrik

Kuat arus listrik ialah banyaknya muatan listrik yang mengalir tiap detik melalui suatu penghantar. Simbol kuat arus adalah I. Satuan kuat arus listrik ialah Ampere (A) yang diambil dari nama seorang ilmuwan Perancis yaitu : Andrey Marie Ampere (1775 - 1836). Kuat arus listrik adalah banyaknya muatan yang mengalir melalui penampang konduktor tiap sekon.

3. Beda Potensial Listrik

Sumber tegangan listrik yaitu peralatan yang dapat menghasilkan beda potensial listrik secara terus menerus. Beda potensial listrik diukur dalam satuan volt (V). Alat yang digunakan adalah volmeter.
Beda potensial adalah banyaknya energi listrik yang diperlukan untuk mengalirkan setiap muatan listrik dari ujung-ujung penghantar disebut beda potensial listrik atau tegangan listrik. Hubungan antara energi listrik, muatan listrik, dan beda potensial listrik secara matematik dirumuskan :

V= W/ Q

Keterangan :

V = Beda potensial listrik dalam volt (V)
W = Energi listrik dalam joule (J)
Q = Muatan listrik dalam coulomb (C)

Arus listrik hanya akan terjadi dalam penghantar jika antara ujung-ujung penghantar terdapat beda potensial (tegangan listrik).

4. Hukum Ohm

Pengertian Hukum Ohm merupakan sebuah teori yang membahas mengenai hubungan antara Tegangan (Volt), Arus (Ampere), dan Hambatan listrik dalam sirkuit (Ohm).

Bunyi hukum Ohm :

"Kuat arus listrik pada suatu beban listrik berbanding lurus dengan tegangan dan berbanding terbalik dengan hambatan".

Rumus Hukum Ohm :
Lambang dari hambatan adalah R, lambang dari Arus adalah I, dan lambang dari tegangan adalah V. Berdasarkan hukum Ohm diatas maka bisa diambil rumus sebagai berikut ini.

Keterangan:

I = Besar arus yang mengalir pada penghantar (A)

V = Besar tegangan pada penghantar (V)

R = Besar hambatan (Ω)

5. Hukum Kirchoff

Pengertian dan Bunyi Hukum Kirchoff 1

Hukum Kirchoff 1 merupakan Hukum Kirchoff yang berkaitan dengan dengan arah arus dalam menghadapi titik percabangan. Hukum Kirchoff 1 ini sering disebut juga dengan Hukum Arus Kirchoff atau Kirchoff’s Current Law (KCL).
Bunyi Hukum Kirchoff 1 adalah sebagai berikut.

“Arus total yang masuk melalui suatu titik percabangan dalam suatu rangkaian listrik sama dengan arus total yang keluar dari titik percabangan tersebut.”

Untuk lebih jelas mengenai bunyi Hukum Kicrhoff 1, silakan lihat rumus dan rangkaian sederhana dibawah ini :

Berdasarkan rangkaian diatas, dapat dirumuskan bahwa :

I₁ + I₂ + I₃ = I₄ + I₅ + I₆

Pengertian dan Bunyi Hukum Kirchoff 2

Hukum Kirchoff 2 merupakan Hukum Kirchoff yang digunakan untuk menganalisis tegangan (beda potensial) komponen-komponen elektronika pada suatu rangkaian tertutup. Hukum Kirchoff 2 ini juga dikenal dengan sebutan Hukum Tegangan Kirchoff atau Kirchoff’s Voltage Law (KVL).

Bunyi Hukum Kirchoff 2 adalah sebagai berikut.

“Total Tegangan (beda potensial) pada suatu rangkaian tertutup adalah nol”

Untuk lebih jelas mengenai bunyi Hukum Kirchoff 2, silakan lihat rumus sederhana dibawah ini berdasarkan rangkaian diatas.

V_ab + V_bc + V_cd+ V_da = 0

6. Kapasitor Pada Rangkaian Arus Searah

A. Pengisian RC (Resistor - Kapasitor).
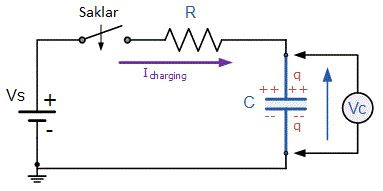
Gambar di bawah menunjukkan sebuah kapasitor, (C) secara seri dengan sebuah resistor, (R) membentuk Rangkaian Pengisian RC yang terhubung melalui supply baterai DC (Vs) melalui saklar mekanis. Saat saklar ditutup, kapasitor secara bertahap akan terisi hingga tegangan mencapai supply tegangan baterai. Cara pengisian kapasitor juga ditunjukkan di bawah ini.

Rangkaian Pengisian RC (Resistor - Kapasitor)

Mari kita asumsikan di atas, bahwa kapasitor (C) sepenuhnya "habis" dan saklar (S) terbuka penuh. Ini adalah kondisi awal dari rangkaian, maka t = 0, i = 0 dan q = 0. Bila saklar ditutup waktu dimulai pada t = 0 dan arus mulai mengalir ke kapasitor melalui resistor.

Karena tegangan awal kapasitor adalah nol, (Vc = 0) kapasitor tampaknya menjadi hubungan pendek ke rangkaian eksternal dan arus mengalir maksimal melalui rangkaian dibatasi hanya oleh resistor. Kemudian dengan menggunakan hukum tegangan Kirchoff (KVL), tegangan turun di sekitar rangkaian diberikan sebagai :

Arus kini mengalir di sekitar rangkaian disebut Pengisian Arus dan ditemukan dengan menggunakan hukum Ohm sebagai: i = Vs / R.

Kurva Rangkaian Pengisian RC

Kapasitor sekarang mulai mengisi seperti yang ditunjukkan, dengan kenaikan pada kurva pengisian RC lebih curam di awal karena tingkat pengisian tercepat di awal dan kemudian mengecil saat kapasitor mengambil isi tambahan pada tingkat yang lebih lambat.

Saat muatan kapasitor naik, perbedaan potensial di pelatnya perlahan meningkat seiring waktu yang sebenarnya diambil untuk muatan pada kapasitor mencapai 63% voltase maksimum yang mungkin, pada kurva 0.63Vs kita dikenal sebagai satu Waktu Konstanta, (T).

Ini 0.63Vs titik tegangan diberikan singkatan dari 1T , (satu waktu konstan).

Kapasitor terus mengisi dan perbedaan voltase antara Vs dan Vc berkurang, jadi untuk menjalankan arus rangkaian, i . Kemudian pada kondisi akhir lebih besar dari lima konstanta waktu (5T) ketika kapasitor dikatakan terisi penuh, t = ∞, i = 0, q = Q = CV. Kemudian pada tak terhingga arus berkurang menjadi nol, kapasitor bertindak seperti kondisi rangkaian terbuka sehingga, turun tegangan seluruhnya melintasi kapasitor.

Jadi secara matematis kita dapat mengatakan bahwa waktu yang dibutuhkan untuk sebuah kapasitor untuk mengisi satu konstanta satu waktu, ( 1T ) diberikan sebagai:

RC Waktu Konstan, Tau - τ

Konstanta waktu RC ini hanya menentukan tingkat pengisian di mana, R ada di Ω dan C di Farad.

Karena tegangan V berhubungan dengan muatan pada kapasitor yang diberikan oleh persamaan, Vc = Q/C , tegangan di seluruh nilai tegangan di kapasitor (Vc) pada waktu mana pun selama periode pengisian diberikan sebagai :

Dimana:
• Vc adalah tegangan kapasitor
• Vs adalah tegangan supply
• t adalah waktu yang telah berlalu sejak penerapan tegangan supply
• RC adalah konstanta waktu dari rangkaian pengisian RC

Setelah satu periode yang sama dengan 4 konstanta waktu, (4T) kapasitor di rangkaian pengisian RC ini hampir terisi penuh dan tegangan di kapasitor sekarang kira-kira 98% dari nilai maksimumnya, 0.98Vs. Jangka waktu yang ditempuh kapasitor untuk mencapai titik 4T ini dikenal sebagai Periode Transien.

Setelah waktu 5T, kapasitor sekarang terisi penuh dan voltase di kapasitor, (Vc) sama dengan voltase supply, (Vs). Karena kapasitor terisi penuh tidak ada arus yang mengalir di rangkaian. Periode waktu setelah titik 5T ini dikenal sebagai Periode Stabil.

B. Pengosongan Kapasitor

Misalkan ada kapasitor yang telah terisi penuh dan masih dalam keadaan terbuka seperti gambar di bawah ini.

Sehingga tegangan antara kedua kaki kapasitor adalah

Ketika saklar ditutup maka muatan dalam kapasitor akan segera mengalir dalam rangkaian. Hal ini mengakibatkan muatan dalam kapasitor berkurang. Muatan yang bergerak dalam rangkaian tak lain adalah arus listrik yang mengalir.